B.1) (somente para alunos da 1a série) Uma das obras brasileiras mais importantes de desenvolvimento sustentável no âmbito nacional é a transposição do rio São Francisco. Ela aproveita parte da água que seria despejada no mar para irrigar 390 municípios do semiárido, beneficiando 12 milhões de pessoas de Pernambuco, Paraíba, Rio Grande do Norte e Ceará. Vemos ao lado a construção de uma barragem que será responsável pela formação de um grande lago que fará parte do complexo relacionado à transposição do rio São Francisco. Essa parede de blocos de 25 m de largura foi planejada para segurar até 200 mil toneladas de água que terá 8m de altura nessa parede. Se o nível da água atingir o máximo, qual a força total que esta parede neutralizará?
|
| Figura extraída em 16/04/2017 em https://paraibaonline.com.br/saiba-como-esta-aevolucao-da-obra-da-transposicao-do-rio-saofrancisco/ |
| |
Sabe-se que a pressão no meio da coluna de água é igual à pressão média que essa parede estaria sofrendo.
Dados: aceleração da gravidade mede 10 m/s² densidade da água = 1 kg/litro e prefixo “Mega” = 10⁶
a) 4 MN
b) 6 MN
c) 8 MN
d) 10 MN
Resolução
B.2)(somente para alunos da 1ª série) Um dos problemas mais graves que o desenvolvimento das atividades humanas trouxe é a falta de água potável. Um exemplo bem significativo disso é um dos piores desastres ambientais do planeta: a desertificação do mar de Aral; este já foi o quarto maior lago do mundo e hoje tem menos de 10% do volume de água que tinha há 50 anos atrás. Projetos russos de irrigação desviaram grande parte dos rios que alimentavam o mar de Aral. Sem a presença dessa massa de água, o clima da região está alterando com verões cada vez mais quentes e secos e com invernos cada vez mais frios e longos. ]
Figura extraída em 20/04/2017em https://pt.wikipedia.org/wiki/Mar_de_Aral#/med ia/File:Aral_Sea_1989-2008.jpg
Atualmente as temperaturas máximas e mínimas da região atingem valores desconfortantes: 5 °F e 113 °F. Tendo como referência os dados acima e sabendo que a temperatura de fusão do gelo é igual a 32 °F e a temperatura de ebulição da água é igual a 212 °F, quais as indicações para as temperaturas 5 °F e 113 °F, respectivamente, na escala Celsius?
a) – 20 °C e 45 °C
b) – 20 °C e 35 °C
c) – 15 °C e 45°C
d) – 15 °C e 35°C
B.3) (somente para alunos da 1a série) Uma das formas de reduzir a emissão de CO2 (um dos responsáveis pelo aquecimento global) é substituir a queima de combustíveis fósseis (butano, madeira, carvão, etc) pela energia solar na geração de calor. A utilização de fogões solares para a feitura de alimentos nos dias sem muitas nuvens é uma prática colaborativa para a sustentabilidade. Um modelo eficiente de fogão solar é constituído basicamente por uma calota espelhada na parte côncava e a panela localizada à sua frente. Para ter melhor eficiência, o projeto deveria possibilitar a mudança da posição da calota conforme figura abaixo.
Qual a ação que NÃO iria aumentar a eficiência do aquecimento da panela?
a) O eixo principal deve estar apontado para o Sol.
b) A panela deve estar localizada no centro de curvatura.
c) A parte externa da panela deve estar pintada de preto.
d) A forma da calota deve ser parabólica.
Alternativa B. A panela não deve estar no centro de curvatura, pois não receberia tanta incidência dos raios solares. Seguindo o esquema do que acontece em espelho esférico: Percebemos que colocar o objeto no centro não aumentaria a eficiência do fogão. Pois, os raios que incidem paralelamente passam pelo Foco e não pelo centro de curvatura.
B.4) (somente para alunos da 1a série) O aquecimento global mexe com as correntes marítimas que podem interferir na dinâmica térmica de todo o planeta. Um exemplo disso é o da geleira PROT-C. Ela fica próxima à Antártica, no sul da Argentina e é dividida em dois pedaços, Oeste e Leste. O pedaço Leste fica sobre uma ilha oceânica mantendo toda a geleira fixa. As correntes que contornam essa geleira vinham da Antártica durante todo o ano, logo eram correntes de águas frias. Nos últimos anos, devido às mudanças climáticas, no verão, passa uma corrente de água quente costeando o lado oeste. Nesse período, o lado Oeste varia de uma temperatura de – 12 °C para – 2 °C enquanto o lado Leste passa de uma temperatura de -12 °C para – 10°C . Os dois lados sofrem dilatações térmicas diferentes, o que produz uma rachadura na linha AB de 200 km que separa os dois lados. Isso acaba descolando o lado Oeste que se transformará em um grande Iceberg no verão e será levado para o Norte durante o inverno. Ao chegar em regiões mais quentes, esse Iceberg será derretido.

Considerando o texto acima, qual a diferença da dilatação do comprimento AB em cada lado dessa geleira durante o verão? Dado: coeficiente de dilatação volumétrico do gelo = 153x10^-6 °C^-1
a) 81,6 m
b) 82,5 m
c) 86,4 m
d) 88,2 m
Resolução:
B.5) (somente para alunos da 1a série) Um próspero campo de produção de energia limpa está sendo explorado nos últimos anos: a energia marítima. O Brasil é um dos pioneiros nessa nova tecnologia. A 60 km de Fortaleza (CE) está sendo testada a primeira usina de ondas da América Latina, um projeto exclusivamente brasileiro. A extremidade de um braço mecânico de 24 m fica apoiada em um flutuador que sobe e desce de acordo com as ondas. Esse movimento é transmitido ao pistão de uma bomba hidráulica que fica a 2 m do eixo de rotação do braço mecânico. A bomba hidráulica movimenta um gerador de energia elétrica.
 |
| Extraído em 08/05/2017 em https://milenar.org/category/1-parte-primeira/5-secao-quinta/3-energias-renovaveis/energia-das-mares/ |
Desprezando o peso do braço mecânico, quando o flutuador aplica na extremidade do braço uma força de 6.000 N, qual a intensidade de força que o pistão da bomba hidráulica sofre aplicado pelo braço mecânico? Considere que o sistema está em equilíbrio
a) 500 N
b) 800 N
c) 36 kN
d) 72 kN
Resolução:

B.6) “Desenvolvimento sustentável”, “sustentabilidade”, “energia limpa”, “biocombustíveis” e “tecnologia sustentável” são alguns conceitos que surgiram nas últimas décadas após as fortes evidências do impacto produzido pela interferência da humanidade na natureza. Vivemos em uma balança desequilibrada que, de um lado pesa a preservação da natureza e do outro pesa (com mais intensidade) o desenvolvimento econômico. Contudo, muitos especialistas apostam que a tecnologia pode estabelecer um equilíbrio. Concernente a isso, o Brasil teve um papel central nas discussões sobre o desenvolvimento sustentável no mundo, sendo sede das últimas conferências organizadas pela ONU sobre o tema: a RIO 92 e a RIO+20. Com a presença maciça dos países integrantes dessa organização, uma das resoluções esperadas para essas conferências é a definição de Objetivos do Desenvolvimento Sustentável (ODS) que para serem conquistados precisarão de toda a potencialidade criativa das ciências da natureza na produção de novas tecnologias. Existe um desses objetivos que dialoga mais diretamente com a Física e que está presente em uma das proposições abaixo. Identifique-o.
a) Segurança sustentável da água. Acesso universal à água potável e saneamento básico; garantia de eficiência maior na gestão dos recursos hidrominerais.
b) Energia limpa universal. Aumentar o acesso universal à energia limpa, minimizando a poluição e o impacto à saúde, além de reduzir o impacto do aquecimento global.
c) Ecossistemas produtivos e saudáveis. Assegurar os serviços ecossistêmicos e da biodiversidade com uma melhor gestão, restauro e conservação do meio ambiente.
d) Segurança alimentar sustentável. Fim da fome e alcance a longo prazo da segurança na produção de alimentos, com distribuição e consumo sustentáveis.
Solução: A física está extremamente ligada com a produção de energia limpa e universal, o termo “limpa”, por ser fontes renováveis e que não prejudiquem o meio ambiente como: Energia eólica, energia solar. E o termo “universal” é como forma de garantia da dissipação de energia sustentável para grande parte do mundo. Como garantia de uma melhora geral para as pessoas e o planeta seria reduzido a quantidades de gases poluentes que fazem mal para a saúde e quando retidos em altas quantidades na atmosfera aumento o efeito estufa.
B.7) Um dos problemas trazidos pelo desenvolvimento da humanidade é a intensificação do efeito estufa na atmosfera. Acontece que o efeito estufa é um fenômeno natural que mantém a Terra aquecida. A figura abaixo mostra de forma simplificada a relação entre radiação e atmosfera. A radiação solar passa totalmente do espaço para a atmosfera. Chegando à superfície da Terra, essa radiação, em sua maioria, é refletida, retornando ao espaço. O que não é refletido é absorvido em forma de calor. A superfície da Terra também emite radiação em uma quantidade maior que a radiação solar absorvida. A radiação terrestre tem características diferentes da radiação solar. Alguns gases que compõem a atmosfera, como o gás carbônico, deixam a radiação solar passar, mas refletem a radiação terrestre. Essa propriedade é chamada de “efeito estufa”. É esse efeito que faz grande parte da radiação terrestre voltar para a Terra evitando que esse calor seja perdido para o espaço. Além disso, a queima de matéria orgânica (madeira, carvão e combustíveis fósseis em geral) produz gás carbônico, intensificando o efeito estufa.

Baseado no enunciado, determine a proposição que corresponde a algo que não iria acontecer, se a quantidade de gases que produzem o efeito estufa aumentasse muito.
a) A quantidade de radiação terrestre refletida aumentaria, logo sairia menor “quantidade de calor que o calor absorvido pela Terra”, a qual sofreria aquecimento.
b) A grande quantidade de gelo das calotas polares iria derreter, aumentando o nível dos oceanos.
c) Aumentaria a quantidade de vapor no ar (umidade do ar) o que alteraria o clima do planeta na
medida em que mudaria a dinâmica das precipitações atmosféricas.
d) Aumentaria a quantidade de radiação solar que atingiria a superfície da Terra.
Solução: Por eliminação: O item A, está correto, pois com o acumulo de gases e o aumento do efeito estufa, a radiação terrestre que deveria ser refletida de volta ao espaço voltaria em menor quantidade, pois em sua maioria ficaria retida na atmosfera terrestre. O item B, também ocorreria como se é divulgado o aquecimento global provoca o derretimento de geleiras e calotas polares o que faz o nível do oceano aumentar. O item C, também ocorreria, pois as mudanças climáticas são decorrentes do aumento do efeito estufa. O item D é o único que não aconteceria em relação ao efeito estufa, pois mesmo com os gases na atmosfera a radiação que chega na Terra seria a mesma, não aumentaria e nem reduziria. Ou seja, como sugere a figura os gases da atmosfera permitem tranquilamente a passagem da radiação vinda de fora.
B.8) Um dos problemas ambientais vivenciados mundialmente é o aquecimento global. Muitos especialistas defendem que sua causa é o acelerado desenvolvimento humano estimulado pelo desenfreado crescimento econômico. Portanto, isso faz parte de um dos graves problemas que o desenvolvimento sustentável tem de resolver.
Figura abaixo e à esquerda foi extraída em 20/04/2017 emhttp://brasilescola.uol.com.br/geografia/eclipse-solar.htm
Figura acima e à direita foi extraída em 20/04/2017 em http://fisicanaveia.blogosfera.uol.com.br/tag/eclipse/
A Lua completa seu ciclo em 27 dias, mas o plano que contém a sua órbita não contém o Sol. É por isso que o eclipse solar é algo raro. Um aluno sugeriu, como uma ação para reduzir o aquecimento global, colocar a órbita da Lua no mesmo plano da órbita da Terra e reduzir o raio de sua trajetória, assim aumentaria a quantidade de eclipses solares e aumentaria o tamanho da sombra da Lua na Terra.
Se fosse possível fazer tais alterações, determine a proposição falsa caso elas fossem realizadas.
a) Ocorreriam 13 eclipses solares durante o ano.
b) A diferença entre a altura da maré cheia e a da maré vazia aumentaria.
c) Seria necessário aumentar a velocidade da Lua para que ela descrevesse um MCU.
d) O período de translação da Lua diminuiria.
Solução: Alternativa A. Caso fosse possível fazer tal mudança o número de eclipses seria menor que 13. Pois, ocorreria um eclipse a cada mês terrestre.
B.9) O gás carbônico é o gás do efeito estufa mais produzido pelo desenvolvimento humano. Além da respiração, ele é emitido quando queimamos compostos orgânicos como madeira, carvão e combustíveis em geral (gasolina, etano, diesel etc.). O controle da emissão de gás carbônico é tão importante que muitos órgãos governamentais passaram a medir a poluição produzida por um país ou por uma empresa a partir desse gás. Assim foi criada a unidade “crédito de carbono” que equivale à redução da emissão de uma tonelada de gás carbônico na atmosfera. Muitos governos oferecem incentivos fiscais para as empresas que ganharem créditos de carbono. Essas ações tentam reduzir os efeitos do aquecimento global, como o desgelo que está ocorrendo nas calotas polares e que gera aumento no nível dos oceanos.
Sobre esse assunto, determine a proposição verdadeira:
a) Um iceberg (água doce solidificada), ao derreter completamente, não aumenta o nível de água, pois a água que surge do derretimento ocupará exatamente o volume do iceberg que estava imerso na água.
b) Um iceberg (água doce solidificada), ao derreter completamente, aumenta o nível da água do mar, pois a água que surge do derretimento ocupará mais que o volume imerso do iceberg.
c) A água doce que surge do iceberg em derretimento possui uma densidade maior que a água salgada.
d) O derretimento do gelo que está boiando no oceano altera mais o nível dos oceanos que o derretimento do gelo que está sobre o solo firme.
Solução: Alternativa B. A água dos icebergs não é salgada como a intuição sugere, são feitos de água doce solidificada, icebergs são pedaços de gelo que se desprendem de geleiras e vagam pelo oceano. Quando há o derretimento destes volume do nível do mar aumenta.
B.10) Quando se fala em sustentabilidade, é necessário fazer o controle dos impactos ambientais que a ação do homem poderá produzir. Os rios são recursos naturais estratégicos para medir essa interferência. Existem várias maneiras de fazer o monitoramento da qualidade da água. Algumas são excelentes para identificar um agente agressor como é o caso da resina usada para tintas acrílicas. Essa resina é altamente tóxica para um rio. Apesar de possuir uma densidade muito parecida com a da água, sua natureza eletromagnética aumenta significativamente o índice de refração (n), o que sugere utilizar um equipamento óptico para identificar sua presença.

Em um rio nas margens de uma indústria química que fabrica essa resina, usa-se um equipamento flutuante contendo um laser em um recipiente transparente, conforme figura apresentada. Ao acionar o equipamento, ele liga o laser cuja luz atinge uma placa detectora. O equipamento faz a leitura e emite avisos de segurança conforme referência abaixo. Certo dia, esse dispositivo mostrou o caminho do raio de luz do laser conforme imagem.
Determine o aviso emitido pelo equipamento nesse dia.
a) Normal (n < 1,5)
b) Atenção (1,5 ≤ n < 2,0)
c) Perigo de contaminação (2,0 ≤ n < 3,5)
d) Rio contaminado (n ≥ 3,5)
Resolução

B.11) Além de promover a fotossíntese e acolher ecossistemas, uma floresta ajuda na evaporação, interferindo no controle de temperatura e no regime de chuvas de uma região. A exploração econômica desenfreada de uma floresta pode fazê-la desaparecer. Assim, o combate ao desmatamento ilegal na maior floresta tropical do mundo, a Amazônica, é uma das mais importantes ações brasileiras para o desenvolvimento sustentável. Contudo, além do desmatamento destruir a floresta nativa, ele chegou a ser responsável por 60% da poluição anual que o Brasil lançou na atmosfera. Medidas relacionadas a isso foram tomadas e, nos últimos anos, o Plano de Ação para a Prevenção e Controle do Desmatamento da Amazônia Legal (PPCDAm), por exemplo, reduziu, em média, 75% a taxa de desmatamento anual. O PPCDAm conta com um dos maiores sistemas de monitoramento do mundo, operando com ajuda de satélites equipados exclusivamente para esse fim. O CBERS-1 e o CBERS-2 são satélites que fazem parte desse sistema. Eles foram colocados em órbita por meio de foguetes chineses, pois não possuem sistemas de propulsão. Para que se tornassem geoestacionários, ficando sempre sobre a região amazônica e descrevendo MCUs, foram lançados com 12.000 km/h em um local cuja aceleração da gravidade mede 3.000 km/h2. Obedecendo os dados oferecidos e considerando que o raio da Terra mede 6.000 km, qual a altitude das
órbitas desses satélites?
a) 36.000 km
b) 42.000 km
c) 46.000 km
d) 52.000 km
Resolução
B.12) Cerca de 70% da matriz energética brasileira atual é hidroelétrica. Esse índice era bem maior graças ao modelo de usinas hidroelétricas acopladas a grandes reservatórios, adotado até a década de 90. Entretanto, as grandes áreas inundadas produziam um enorme impacto ambiental. Por essa razão, atualmente, o modelo usado abandona a construção de grandes reservatórios para preservar o curso do rio. Entretanto, o fluxo de água de um rio varia muito durante o ano. Na região amazônica, que guarda o maior potencial hidroelétrico não explorado do Brasil, existem rios cuja diferença entre a maior e a menor vazão chega a ser de 25 vezes. O reservatório serve para compensar essa diferença. Sem os reservatórios, o Brasil teria que acionar termoelétricas nos períodos de baixo fluxo de água. Porém as termoelétricas poluem o ar com a queima de combustível.

Considere que seja executado um empreendimento no rio Cana Brava, afluente do rio Tocantins, em que duas usinas, uma hidroelétrica e outra termoelétrica, sejam construídas para trabalharem em parceria. A hidroelétrica seria construída em um local desse rio onde existe uma queda d’água de 40 m. Esse rio possui vazão máxima de 2.000.000 kg/s e vazão mínima é 400.000 kg/s.
Digamos que:
- para cada 1 kg de gás carbônico liberado por essa termoelétrica, ela produza 64 MJ de energia;
- a vazão do rio não seja alterada para não inundar as margens originais;
- o processo de transformação de energia mecânica em energia elétrica tenha um rendimento 100%.
Quanto tempo levaria, no período de baixa vazão, para que esse empreendimento perdesse 1 crédito de carbono (veja questão B.9) produzindo a mesma quantidade de energia que no período de alta vazão, quando a termoelétrica estaria desligada?
Dados: aceleração da gravidade = 10 m/s2
Prefixo “Mega” = 10⁶
a) 1 min e 40 s
b) 2 min e 0 s
c) 2 min e 20 s
d)2 min e 30 s
Resolução

B.13) O governo de Pernambuco está apostando no desenvolvimento sustentável ao financiar cinco projetos de usinas de energia elétrica com baixo impacto ambiental. Essas usinas são termosolares, construídas em regiões do semiárido com pouca presença de nuvens. O princípio básico é usar espelhos côncavos cilíndricos para focalizar a luz do Sol em uma tubulação por onde passa água. A água vira vapor que continuaria sendo aquecido atingindo altas pressões. O vapor é liberado em direção a uma turbina que move um gerador de energia elétrica. Além de usar uma fonte de energia limpa, a construção dessa usina é mais barata que a de usinas com células fotovoltaicas. O conceito de energia limpa ainda é controverso, mas podemos adotar que é o processo de produção de energia que não lança poluentes na atmosfera e produz impacto sobre a natureza somente no local da instalação da usina. Se a incidência solar é de 0,2 kW/m2, uma usina termosolar, cujos espelhos ocupassem 600.000 m2, teria uma potência de produção de energia elétrica igual a 80.000 kW.
 |
| Figura extraída em 15/04/2017em | http://www.pe.gov.br/blog/2012/06/25/ | convenio-de-r-27-5-milhoes-vaigarantir-construcao-de-usinatermosolar-em-petrolina/ |
Se o calor latente de vaporização da água mede 2.000 kJ/kg e a vazão de água pelos tubos é de 5 kg/s, a vaporização da água representa quantos por cento da potência desperdiçada?
a) 20 %
b) 25 %
c) 25 %
d) 40%
Resolução
B.14) No mundo existem 442 usinas nucleares em funcionamento que são responsáveis por 6,4 % da energia elétrica produzida. É claro que acidentes como o de Chernobyl (em 1986) e o do Japão (em 2011) trazem muita desconfiança quanto à segurança de tais usinas. Certamente, as vantagens das usinas nucleares devem superar a possibilidade de um desastre, haja vista que os Estados Unidos (104 usinas) e o Japão (54 usinas), referências de industrialização no mundo, utilizam largamente esse recurso. O fato, porém, é que a energia nuclear é considerada uma forma de energia limpa. Vejamos como funciona uma usina nuclear. Seu coração é o reator, onde energia nuclear do urânio é transformada em calor. O reator também libera radiação nuclear, mas essa é blindada por diversas paredes de contenção. Daí para frente ocorre o mesmo que em uma termoelétrica. O calor é usado para aquecer a água do circuito interno da usina. A água vira vapor sob alta pressão que é direcionado para mover uma turbina de um gerador de energia elétrica. Após passar pela turbina, o vapor deve ser transformado em água para voltar ao reator e reiniciar o processo dentro do circuito interno da usina. Essa condensação é feita por um grande volume de água externa vinda de um rio, de um grande lago ou domar. Essa água não se mistura com a água do circuito interno, entretanto, ela retorna à fonte de origem.
 |
| Figura extraída em 15/04/2017em | http://mundoeducacao.bol.uol.com.br/quimica/ | reator-nuclear.htm |
Observe que a energia térmica é a que participa de todos os processos. Por isso, chamamos essas usinas de termonucleares. No caso da nossa usina termonuclear Angra 1, a água do circuito interno absorve 2.000 MW de calor do reator e libera 800 MW de energia mecânica para a turbina que movimenta o gerador. Para que a água desse circuito volte da mesma forma para receber mais calor do reator, 4 toneladas/s de água externa vinda do mar com 15 °C absorvem o calor que não foi absorvido pela turbina em forma de energia mecânica. Essa água externa que retorna ao mar pode ser considerada de poluição física, pois, retorna com uma temperatura que prejudica o ecossistema aquático da região. Determine qual a temperatura dessa água quando retorna ao mar.
Dado: calor específico da água = 4 J/(g. °C)
a) 60 °C
b) 70 °C
c) 80 °C
d) 90 °C
Resolução
B.15) Ainda no campo da “energia limpa”, o Brasil experimentou um crescimento enorme na utilização da energia eólica, principalmente no Rio Grande do Sul, Rio Grande do Norte, Bahia e Ceará. Um aerogerador é um imenso cata-vento como podemos notar na imagem em anexo, em que homens aparecem fazendo a manutenção desse equipamento. Ao liberar a movimentação das hélices do aerogerador, demora um bom intervalo de tempo para que a força do vento faça a hélice ganhar velocidade de trabalho e assim desenvolver um movimento uniforme.
 |
| Figuras extraídas em 16/04/2017 em http://meioambiente.culturamix.com/noticias/beneficios-da-energia-eolica-para-a-humanidade |
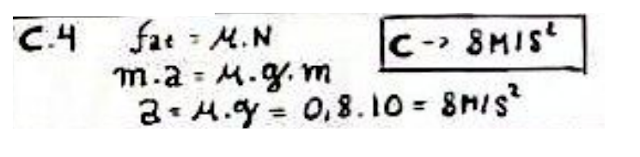
Um dos problemas para a implementação desses equipamentos é a mão de obra especializada e normas de segurança bem definidas para evitar acidentes como o que aconteceu em um aerogerador, onde um técnico subiu até o eixo da hélice com ela em movimento. Devido ao vento, esse técnico, que tinha 90 kg, acabou indo parar na extremidade de uma das pás da hélice preso a um cabo e descrevendo um MCU com aceleração centrípeta igual a 4 m/s². A sorte do técnico é que o cabo não partiu. Qual a intensidade da força máxima que esse cabo suportou? Considere que a aceleração da gravidade mede 10 m/s²
a) 540 N
b) 860 N
c) 1260 N
d) 1340 N
Resolução

B.16) Nosso apanhado sobre atividades que colaboram para o desenvolvimento sustentável não estaria completo se não falássemos de reciclagem. Dentre as técnicas de reciclagem, podemos incluir a utilização do metano (biogás) liberado pela decomposição de matéria orgânica com a construção de biodigestores. A produção de metano é um processo natural e mais abundante nos depósitos de lixo e nas atividades agropecuárias. Como o metano produz cerca de 20 vezes mais efeito estufa que o gás carbônico, a sua utilização como combustível reduz sua presença na atmosfera. Na combustão do metano, é gerada uma molécula de gás carbônico a partir de uma molécula de metano. Como a utilização de biogás como fonte de energia reduz o efeito estufa, ele é considerado uma forma de energia limpa, mesmo liberando gás carbônico na sua combustão. Digamos que o dono de uma fazenda queira implementar uma fonte de energia limpa, mas não possui muito recurso financeiro para investir. Em sua pesquisa sobre o assunto, o dono decidiu usar seus recursos na construção de biodigestores. Entretanto, sua maior necessidade era a produção de energia elétrica para os diversos equipamentos elétricos que utilizava. Considere que a fazenda fique em uma região que possui um regime regular de vento, o que levantou a possibilidade de construir um aerogerador.
 |
| Figura extraída em 16/04/2017 em | http://diybiodigestores.blogspot.com.br/p/biodigestor |
Identifique a proposição que NÃO é um argumento coerente para a escolha de uma dessas formas de energia em relação à outra:
a) A queima do biogás não é muito eficiente na geração de energia elétrica porque os geradores precisam ser movimentados por motores térmicos que possuem baixo rendimento. Os aerogeradores já utilizam o movimento do vento.
b) Com o custo de um aerogerador é possível construir vários biodigestores que poderão gerar a mesma quantidade de energia elétrica além de todos os demais benefícios.
c) Os biodigestores precisam de uma constante introdução de dejetos e retirada de biofertilizantes para que o ritmo da reação química existente não diminua. Já os aerogeradores utilizam um processo autônomo.
d) Acidentes com biodigestores são mais perigosos que com aerogeradores porque estes últimos estão no alto, longe do contato direto com as pessoas e os animais.
Solução: Todos os argumentos dos itens A, B e C. Estão relacionados com eficiência, custo e funcionamento. No item A, é levado em conta o rendimento na produção de energia elétrica, que de fato em um biodigestor é inferior a um aerogerador. O item B relaciona o custo de um aerogerador, a pessoa que deseja utilizar essa fonte de energia gastaria uma quantia superior em comparação com a outra fonte. O Item C, está associado ao trabalho constante que se deve ter para o funcionamento dos biodigestores, ou seja, o que representaria um aumento de funcionários envolvidos.
O último item é o menos coerente para a escolha, pois , acidentes de trabalhos são passiveis de acontecer em qualquer fonte de energia a ser implementada. Este argumento não é plausível suficiente para este tipo de tomada de decisão.
B.17) O controle permanente das condições ambientais inclui o que está acontecendo com a atmosfera. Uma maneira de estudá-la com baixo custo é usar balões meteorológicos. Eles são cheios com hélio ou hidrogênio podendo atingir grandes altitudes. Eles levam equipamento de localização e medição; assim é possível calcular aproximadamente a altura que o balão vai parar de subir. Suponha que um desses balões tinha 5 L de hélio junto ao solo, onde a temperatura era de 27 °C e a pressão atmosférica era de 100 kPa. A força de elasticidade desse balão sempre produzia um aumento de 20 kPa na pressão do hélio do seu interior. O balão subiu até uma altura cuja temperatura era de – 63 °C e a pressão atmosférica era de 10 kPa. Se o balão estava sempre em equilíbrio térmico com a atmosfera da sua vizinhança, quanto o balão dilatou nessa subida?
Dado: 0 K = - 273°C
a) 7 L
b) 8 L
c) 9 L
d) 10 L
Resolução
B.18) Um dos setores produtivos que mais libera gás carbônico na atmosfera é o automobilístico. No ano passado, o governo brasileiro retirou os impostos de importação de carros elétricos apostando que eles seriam uma boa solução para a sustentabilidade nesse setor. Entretanto, a utilização de usinas térmicas na matriz energética do Brasil aumentou. Se por um lado, os carros elétricos não liberam diretamente gás carbônico, pois não se movimentam através da queima de combustíveis, por outro eles vão aumentar o consumo de energia elétrica e a utilização de usinas térmicas. A substituição de carros que usam combustíveis para carros elétricos só será efetiva se a produção de energia elétrica limpa crescer mais que o consumo de energia elétrica. Por isso é tão necessário o estudo da eficiência de carros elétricos.
Imagine que certa distribuidora saiba que um carro popular em média sofra do ar uma força de resistência R cuja intensidade obedece a relação R = 5.v2, determinada para o SI, onde v é a velocidade. Um carro na cidade libera diariamente 1 kg de gás carbônico a cada 100 N de força motriz média para frente produzida pelo sistema de propulsão. Se, em Manaus, os carros desenvolvem uma velocidade média de 72 km/h, quantos créditos de carbono (veja questão B.9) por carro essa distribuidora ganharia por mês quando deixasse de vender carros à combustão e passasse a vender carros elétricos?
Considere que a única força contra o movimento do carro seja produzida pela atmosfera.
a) 0,6 créditos de carbono
b) 0,7 créditos de carbono
c) 0,8 créditos de carbono
d) 0,9 créditos de carbono
Resolução
B.19) Outra maneira de amenizar os efeitos nocivos dos automóveis à combustão é melhorar o rendimento deles. Um automóvel à gasolina funciona sob temperatura máxima de 427 oC e temperatura mínima de 77 °C. Na interpretação de Carnot, podemos considerar que essas temperaturas são as da fonte quente e da fonte fria. A quantidade de gás carbônico liberado por um automóvel que usa gasolina é proporcional ao calor gerado por sua combustão.
Nossos automóveis à gasolina possuem um rendimento de 25 %. Existem pesquisas de novos motores à combustão de gasolina que prometem atingir um rendimento de 4/5 do rendimento máximo para uma máquina térmica trabalhando nessas temperaturas. Se isso acontecesse, qual percentual de carbono os automóveis à gasolina deixariam de emitir para a atmosfera sendo usados da mesma forma pelos usuários?
Dado: 0 K = -273 °C
a) 32,5 %
b) 35,0 %
c) 37,5 %
d) 40,0 %
Resolução
B.20) A rede hidrográfica projetada para a transposição do rio São Francisco é composta por dois eixos: norte e leste. A primeira etapa do eixo norte começa por uma estação de bombeamento em Cabrobó (PE), elevando o rio a uma altura de 39,2 m em relação ao reservatório de Tucutú. Esse primeiro trecho é uma enorme ladeira de 7 km inclinada constantemente de 3,2°. As águas descem esse caminho com uma velocidade constante de 1,4 m/s de acordo com as leis da hidráulica. Se essas águas apostassem corrida com uma esfera partindo do repouso e descendo a mesma ladeira sem qualquer atrito, qual seria a diferença entre os tempos da descida que levariam para percorrer esse percurso?
 |
| Figura extraída em 16/04/2017 em | http://geografialivre.blogspot.com.br/2015/05/a-polemica-transposica |
Dado: aceleração da gravidade = 10 m/s²
a) 4.500 s
b) 4.800 s
c) 5.200 s
d) 5.600 s
Resolução
![]() 0,9
0,9